Matematika Perbandingan Trigonometri pada Segitiga Siku-Siku

 Jika berbicara tentang dasar trigonometri, mutlak kita akan berhadapan dengan segitiga siku-siku, karena trigonometri itu sendiri didefinisikan berdasarkan konsep kesebangunan pada segitiga siku-siku.

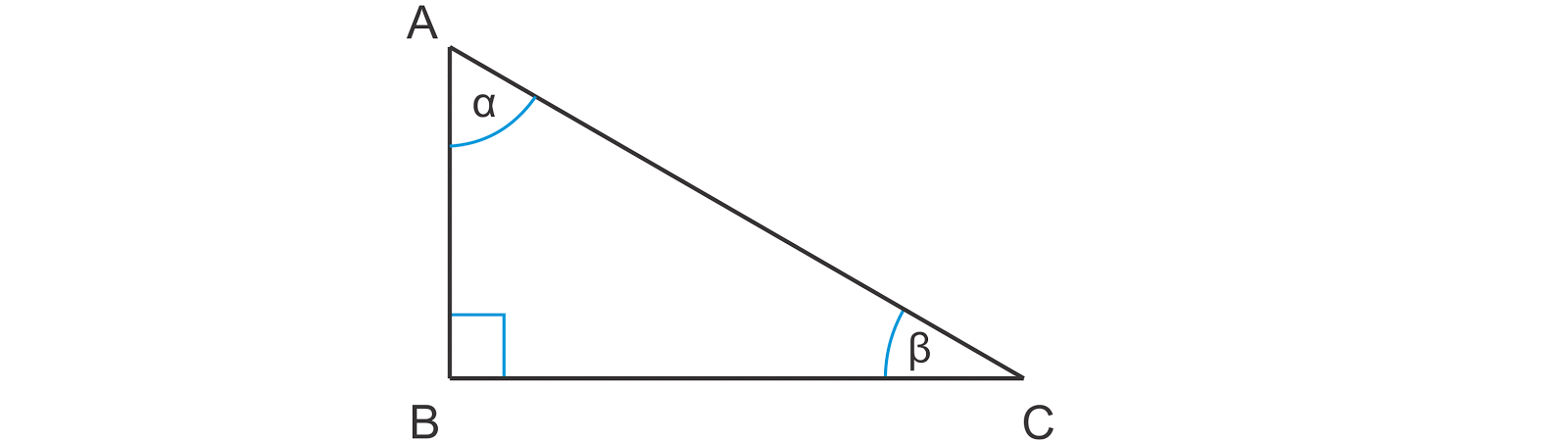
Diberikan segitiga ABC siku-siku di B dengan ∠ A = θ.

Jika sisi di depan sudut (opposite) dinamakan "depan", sisi di samping sudut (adjacent) dinamakan "samping" dan sisi miring (hypotenuse) dinamakan "miring", maka perbandingan sisi-sisi tersebut didefinisikan sebagai berikut :
$$sin\left(\theta \right)=\frac{depan}{miring}csc\left(\theta \right)=\frac{miring}{depan}$$$$cos\left(\theta \right)=\frac{samping}{miring}sec\left(\theta \right)=\frac{miring}{samping}$$$$tan\left(\theta \right)=\frac{depan}{samping}cot\left(\theta \right)=\frac{samping}{depan}$$
Keterangan :
sin untuk sinus
cos untuk cosinus
tan untuk tangen
csc untuk cosecan
sec untuk secan
cot untuk cotangen

Catatan :
Sisi depan dan sisi samping dapat berubah tergantung sudut yang digunakan, sedangkan sisi miring selalu sama, yaitu sisi terpanjang dan letaknya selalu di depan sudut siku-siku.

Dari definisi diatas dapat kita amati dan simpulkan sebagai berikut :

Cosecan adalah kebalikan dari sinus, ditulis$$csc\left(\theta \right)=\frac{1}{sin\left(\theta \right)}$$Secan adalah kebalikan dari cosinus, ditulis$$sec\left(\theta \right)=\frac{1}{cos\left(\theta \right)}$$Cotangen adalah kebalikan dari tangen, ditulis$$cot\left(\theta \right)=\frac{1}{tan\left(\theta \right)}$$
Tangen adalah perbandingan sinus terhadap cosinus, ditulis$$tan\left(\theta \right)=\frac{sin\left(\theta \right)}{cos\left(\theta \right)})$$sehingga$$cot\left(\theta \right)=\frac{cos\left(\theta \right)}{sin\left(\theta \right)}$$

Contoh 1
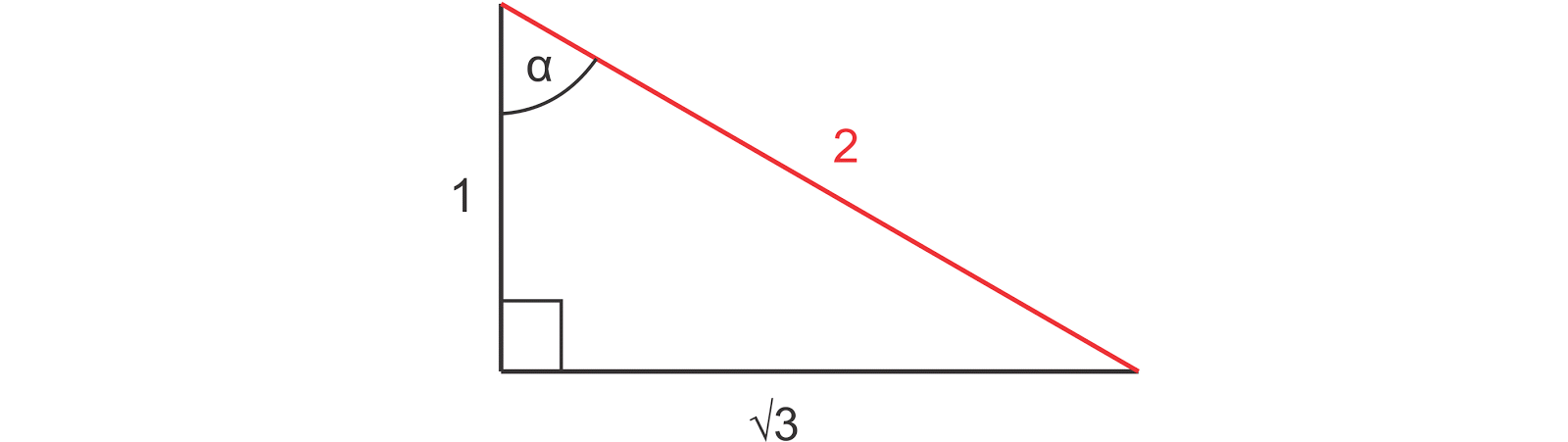
Tentukan semua perbandingan trigonometri untuk sudut α pada segitiga ABC dan sudut β untuk segitiga PQR !

Penyelesaian :
Perhatikan segitiga ABC
AC = $\sqrt{{\left(\sqrt{3}\right)}^2+1^2}$ = 2

Sesuai dengan definisi, maka
sin(α) = $\frac{depan}{miring}$ = $\frac{AB}{AC}$ = $\frac{\sqrt{3}}{2}$
cos(α) = $\frac{samping}{miring}$ = $\frac{BC}{AC}$ = $\frac{1}{2}$
tan(α) = $\frac{depan}{samping}$ = $\frac{AB}{BC}$ = $\frac{\sqrt{3}}{1}$ = $\sqrt{3}$
csc(α) = $\frac{miring}{depan}$ = $\frac{AC}{AB}$ = $\frac{2}{\sqrt{3}}$ = $\frac{2\sqrt{3}}{3}$
sec(α) = $\frac{miring}{smping}$ = $\frac{AC}{BC}$ = $\frac{2}{1}$ = 2
cot(α) = $\frac{samping}{depan}$ = $\frac{BC}{AB}$ = $\frac{1}{\sqrt{3}}$ = $\frac{\sqrt{3}}{3}$

Perhatikan segitiga PQR
QR = $\sqrt{{\left(\sqrt{2}\right)}^2-1^2}$ = 1

Sesuai dengan definisi, maka
sin(β) = $\frac{depan}{miring}$ = $\frac{QR}{PR}$ = $\frac{1}{\sqrt{2}}$ = $\frac{\sqrt{2}}{2}$
cos(β) = $\frac{samping}{miring}$ = $\frac{PQ}{PR}$ = $\frac{1}{\sqrt{2}}$ = $\frac{\sqrt{2}}{2}$
tan(β) = $\frac{depan}{samping}$ = $\frac{QR}{PQ}$ = $\frac{1}{1}$ = 1
csc(β) = $\frac{miring}{depan}$ = $\frac{PR}{QR}$ = $\frac{\sqrt{2}}{1}$ = $\sqrt{2}$
sec(β) = $\frac{miring}{samping}$ = $\frac{PR}{PQ}$ = $\frac{\sqrt{2}}{1}$ = $\sqrt{2}$
cot(β) = $\frac{samping}{depan}$ = $\frac{PQ}{QR}$ = $\frac{1}{1}$ = 1


Contoh 2
Jika tan(α) = $\sqrt{3}$ dan α sudut lancip, tentukan nilai dari $si{n}^2\left(\alpha \right)+co{s}^2\left(\alpha \right)$

Penyelesaian :
tan(α) = $\frac{depan}{samping}$ = $\frac{\sqrt{3}}{1}$

Karena perbandingan trigonometri memenuhi konsep kesebangunan, dapat ditulis :
depan = $\sqrt{3}$
samping = 1

Dengan teorema phytagoras
miring = $\sqrt{(\sqrt{3}{)}^2+1^2}$ = 2

Berdasarkan definisi, kita peroleh
sin(α) =  $\frac{\sqrt{3}}{2}$
cos(α) = $\frac{1}{2}$

sin²(α) + cos²(α) = ($\frac{\sqrt{3}}{2}$)² + ($\frac{1}{2}$)²
sin²(α) + cos²(α) = $\frac{3}{4}$ + $\frac{1}{4}$
sin²(α) + cos²(α) = 1

Jadi, sin²(α) + cos²(α) = 1


Contoh 3
Jika sin(β) = $\frac{1}{2}$ dan sudut β lancip, tentukan nilai dari $se{c}^2\left(\beta \right)-ta{n}^2\left(\beta \right)$

Penyelesaian :
sin(β) = $\frac{depan}{miring}$ = $\frac{1}{2}$

depan = 1
miring = 2
samping = $\sqrt{2^2-1^2}$ = $\sqrt{3}$

Sesuai definisi
sec(β) = $\frac{2}{\sqrt{3}}$
tan(β) = $\frac{1}{\sqrt{3}}$

sec²(β) − tan²(β) = ($\frac{2}{\sqrt{3}}$)² − ($\frac{1}{\sqrt{3}}$)²
sec²(α) − tan²(α) = $\frac{4}{3}$ − $\frac{1}{3}$
sec²(α) − tan²(α) = 1

Jadi, sec²(β) − tan²(β) = 1


Contoh 4
Jika cos(γ) = $\frac{\sqrt{2}}{2}$ dan sudut γ lancip, tentukan nilai dari $cs{c}^2\left(\gamma \right)-co{t}^2\left(\gamma \right)$

Penyelesaian :
cos(γ) = $\frac{samping}{miring}$ = $\frac{\sqrt{2}}{2}$
samping = $\sqrt{2}$
miring = 2
depan = $\sqrt{2^2-(\sqrt{2}{)}^2}$ = $\sqrt{2}$

Sesuai definisi
csc(γ) = $\frac{2}{\sqrt{2}}$
cot(γ) = $\frac{\sqrt{2}}{\sqrt{2}}$ = 1

csc²(γ) − cot²(γ) = ($\frac{2}{\sqrt{2}}$)²  − (1)²
csc²(γ) − cot²(α) = 2 − 1
csc²(γ) − cot²(α) = 1

Jadi, csc²(γ) − cot²(γ) = 1


Contoh 5
Diberikan segitiga ABC $\perp B$ dengan $\angle A=\alpha$ dan $\angle C=\beta$. Tunjukkan bahwa $sin\left(\alpha \right)=cos({90}^{\circ }-\alpha )$ dan $cos\left(\beta \right)=sin({90}^{\circ }-\beta )$

Penyelesaian :

Sesuai definisi, maka
sin(α) = $\frac{BC}{AC}$
cos(β) = $\frac{BC}{AC}$

Dari kedua persamaan diatas, maka
sin(α) = cos(β)  ......................................(1)

∠A + ∠B + ∠C = 180°
α + 90° + β = 180°
α + β = 90°
α = 90° − β  .............................(2)

β = 90° − α  .............................(3)

Substitusi (2) ke (1) diperoleh
sin(90° − β) = cos(β)

Substitusi (3) ke (1) diperoleh
sin(α) = cos(90° − α)

Contoh 6
Diketahui segitiga ABC $\perp B$. Titik D terletak pada BC sehingga $CD=1$. Jika $\angle ADB=\alpha$ dan $\angle ACB=\beta$, tunjukkan bahwa $AB=\frac{tan\left(\alpha \right)tan\left(\beta \right)}{tan\left(\alpha \right)-tan\left(\beta \right)}$

Penyelesaian :

Perhatikan segitiga ABD
tan(α) = $\frac{AB}{BD}$
⇔ AB = BD tan(α)  ................................(1)

Perhatikan segitiga ABC
tan(β) = $\frac{AB}{BD+1}$
⇔ AB = (BD + 1) tan(β)  .......................(2)

Dari persamaan (1) dan (2)
BD tan(α) = (BD + 1) tan(β)
BD tan(α) = BD tan(β) + tan(β)
BD tan(α) − BD tan(β) = tan(β)
BD(tan(α) − tan(β)) = tan(β)
BD = $\frac{tan\left(\beta \right)}{tan\left(\alpha \right)-tan\left(\beta \right)}$  ..................................(3)

Substitusi (3) ke (1)
AB = $\frac{tan\left(\beta \right)}{tan\left(\alpha \right)-tan\left(\beta \right)}$ tan(α)

diperoleh
AB = $\frac{tan\left(\alpha \right)tan\left(\beta \right)}{tan\left(\alpha \right)-tan\left(\beta \right)}$

sumber: https://smatika.blogspot.com/

Share this post