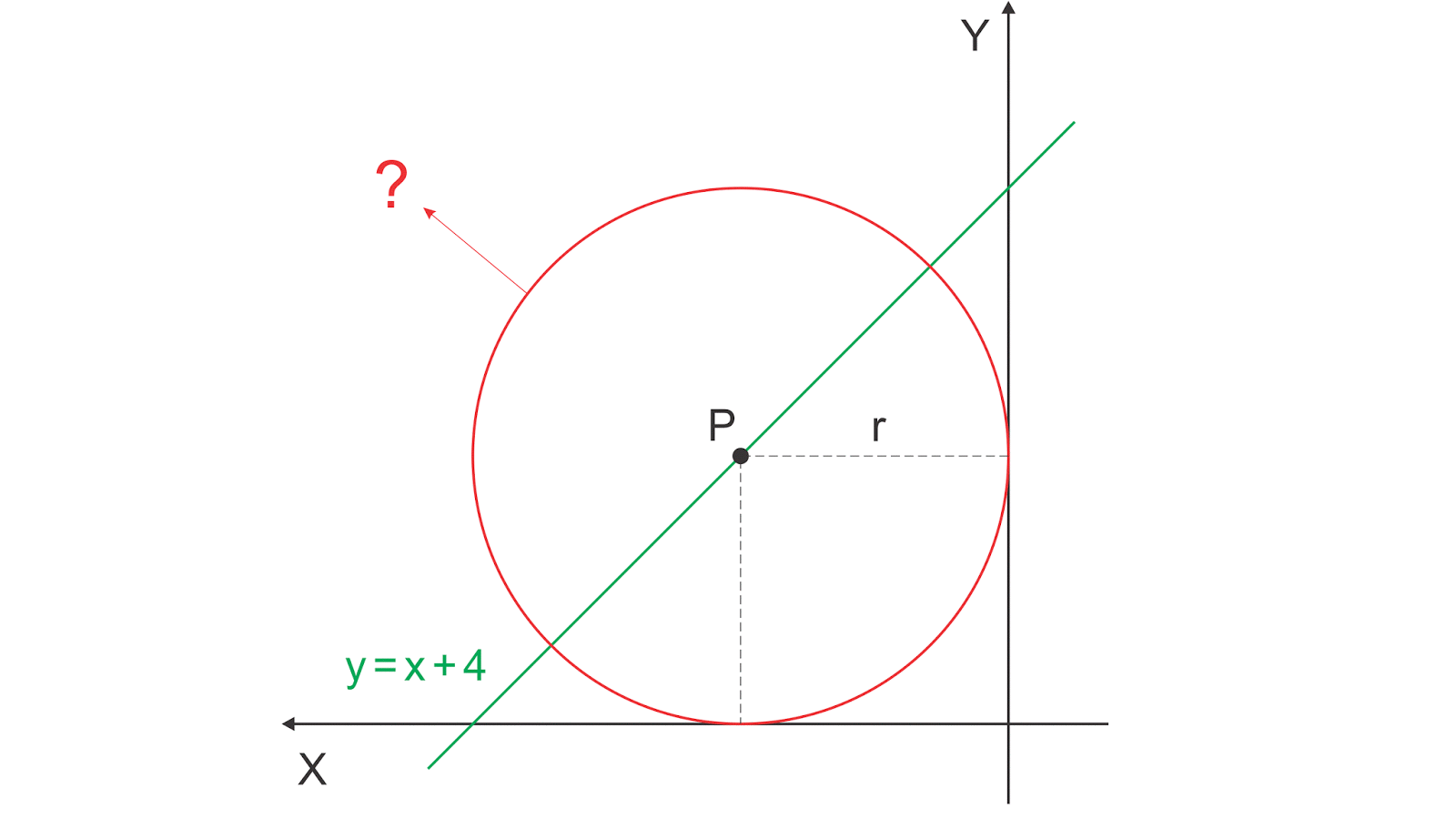Persamaan Lingkaran (Matematika)

 

Persamaan lingkaran dengan pusat (0, 0) dan jari-jari r adalah

x² + y² = r²

Persamaan lingkaran dengan pusat (a, b) dan jari-jari r adalah

(x - a)² + (y - b)² = r²

Persamaan diatas sering disebut dengan bentuk baku persamaan lingkaran.

Contoh 1
Tentukan pusat dan jari-jari lingkaran berikut!
a.  x² + y² = 9

    Jawab :
    P(0,0)
    r = √9 = 3

b.  4x² + 4y² = 100

    Jawab :
    4x² + 4y² = 100  ⇔  x² + y² = 25
    P(0, 0)
    r = √25 = 5

c.  (x − 1)² + (y − 2)² = 12

    Jawab :
    P(1, 2)
    r = √12 = 2√3

d.  (x + 3)² + (y − 4)² = 16

     Jawab :
     P(−3, 4)
     r = √16 = 4



Contoh 2
Tentukan persamaan lingkaran jika diketahui :
a.  P(0, 0) ; r = 7

    Jawab :
    x² + y² = 7²
    x² + y² = 49

b.  P(2, −2) ; r = 3√2

    Jawab :
    (x − 2)² + (y + 2)² = (3√2)²
    (x − 2)² + (y + 2)² = 18


Selain dalam bentuk baku diatas, persamaan lingkaran dapat pula dinyatakan dalam bentuk umum sebagai berikut :

x² + y² + Ax + By + C= 0

dengan pusat dan jari-jarinya adalah

$P=\left(-\frac{A}{2},-\frac{B}{2}\right)$

$r=\sqrt{\frac{A^2}{4}+\frac{B^2}{4}-C}$

Contoh 3
Tentukan bentuk umum persamaan lingkaran yang berpusat di P(−1, 3) dengan jari-jari 7 !

Jawab :
(x + 1)² + (y − 3)² = 7²
x² + 2x + 1 + y² − 6y + 9 = 49
x² + y² + 2x − 6y − 39 = 0

Contoh 4
Tentukan pusat dan jari-jari lingkaran $x^2+y^2-6x+2y-15=0$ !

Jawab :
A = −6 ; B = 2 ; C = −15

Pusat lingkaran :
P$(-\frac{A}{2},-\frac{B}{2})$
P$(-\frac{(-6)}{2},-\frac{2}{2})$ ⇔ P(3, −1)

Jari-jari lingkaran :
r = $\sqrt{\frac{A^2}{4}+\frac{B^2}{4}-C}$
r = $\sqrt{\frac{(-6{)}^2}{4}+\frac{2^2}{4}-(-15)}$ = 5

Latihan Soal Persamaan Lingkaran

Latihan 1
Persamaan lingkaran yang berpusat di (−2, 1) dan melalui titik (1, 5) adalah...

Jawab :

Persamaan lingkaran dengan pusat (−2, 1) dan jari-jari r adalah :
(x + 2)² + (y − 1)² = r²

Lingkaran melalui titik (1, 5) sehingga :
(1 + 2)² + (5 − 1)² = r²
25 = r²

Jadi, persamaan lingkaran :
(x + 2)² + (y − 1)² = 25

atau dalam bentuk umum :
x² + y² + 4x − 2y − 20 = 0


Latihan 2
Jika diameter suatu lingkaran adalah AB dengan titik A(4, 5) dan B(0, −3), tentukan persamaan lingkaran tersebut !

Jawab :

Diameter adalah jarak titik A ke titik B :
d = AB = $\sqrt{(4-0{)}^2+(5-(-3){)}^2}$ = $\sqrt{80}$

Jari-jari adalah setengah dari diameter :
r = $\frac{1}{2}$$\sqrt{80}$

Pusat lingkaran adalah titik tengah AB :
P$\left(\frac{4+0}{2},\frac{5+(-3)}{2}\right)$ ⇔ P(2, 1)

Jadi, persamaan lingkaran :
(x − 2)² + (y − 1)² = ${\left(\frac{1}{2}\sqrt{80}\right)}^2$
(x − 2)² + (y − 1)² = 20

atau dalam bentuk umum :
x² + y² − 4x − 2y − 15 = 0


Latihan 3
Persamaan lingkaran yang berpusat di (−2, 3) dan menyinggung garis $x+2y+6=0$ adalah...

Jawab :

INGAT :
Jarak titik (x₁, x₂) ke garis $ax+by+c=0$ adalah
d = $\left|\frac{a{x}_1+b{y}_1+c}{\sqrt{a^2+b^2}}\right|$

Jari-jari adalah jarak dari titik pusat (−2, 3) ke garis $x+2y+6=0$.
r = $\left|\frac{1(-2)+2\left(3\right)+6}{\sqrt{1^2+2^2}}\right|$ = 2$\sqrt{5}$

Jadi, persamaan lingkaran :
(x + 2)² + (y − 3)² = ${\left(2\sqrt{5}\right)}^2$
(x + 2)² + (y − 3)² = 20

atau dalam bentuk umum :
x² + y² + 4x − 6y − 7 = 0


Latihan 4
Jika garis y = 2x + p menyinggung lingkaran $x^2+y^2-6x-4y+8=0$, tentukan nilai p !

Jawab :

Substitusi y = 2x + p ke persamaan lingkaran :
x² + y² − 6x − 4y + 8 = 0
x² + (2x + p)² − 6x − 4(2x + p) + 8 = 0
5x² + (4p − 14)x + p² − 4p + 8 = 0

Garis menyinggung lingkaran, maka :
D = 0
b² − 4ac = 0
(4p − 14)² − 4.5.(p² − 4p + 8) = 0
p² + 8p − 9 = 0
(p + 9)(p − 1) = 0
p = −9 atau p = 1


Latihan 5
Tentukan persamaan lingkaran dengan pusat (3, 4) dan lingkaran tersebut
a. menyinggung sumbu-x
b. menyinggung sumbu-y

Jawab :

a.  P(3, 4) dan menyinggung sumbu-x, maka
     r = 4

     Persamaan lingkaran :
     (x − 3)² + (y − 4)² = 4²
     (x − 3)² + (y − 4)² = 16

     atau dalam bentuk umum :
     x² + y² − 6x − 8y + 9 = 0

b.  P(3, 4) dan menyinggung sumbu-y, maka
     r = 3

     Persamaan lingkaran :
     (x − 3)² + (y − 4)² = 3²
     (x − 3)² + (y − 4)² = 9

     atau dalam bentuk umum :
     x² + y² − 6x − 8y + 16 = 0


Latihan 6
Tentukan persamaan lingkaran yang pusatnya terletak pada garis $y=x+4$ serta menyinggung sumbu-x negatif dan sumbu-y positif !

Jawab :

Lingkaran menyinggung sumbu-x negatif dan sumbu-y positif, sehingga pusatnya dapat ditulis :
P(−a, b) dengan a = b.

Karena P(−a, b) terletak pada garis $y=x+4$ maka
b = −a + 4

Karena a = b maka
b = −a + 4
a = −a + 4
a = 2

Diperoleh a = b = 2

Sehingga pusat lingkaran tersebut adalah :
P(−a, b) ⇔ P(−2, 2)

Karena lingkaran menyinggung kedua sumbu, maka
r = |a| = |b| = 2

Jadi, persamaan lingkaran :
(x + 2)² + (y − 2)² = 2²
(x + 2)² + (y − 2)² = 4

atau dalam bentuk umum :
x² + y² + 4x − 4y + 4 = 0

sumber: https://smatika.blogspot.com/

Share this post